Home Research Teaching Images Computations

Illustrations

You can copy any of my images in order to use it as an illustration for your presentations, pre-print, courses, exercises, etc. However, before submitting a paper for publication, if you are using one of my images, please email me to ask permission (I will almost surely say "yes").

When reproducing one of these images, please cite my name (G. Poullot), and, if time and space allows use, cite the year, and/or the article the image is extracted from.

Use right-click to save an image as SVG, or click to open the image as a PDF in a new tab (reciprocaly GIF for animations). If you want the LaTeX version of an image, please email me.

Animations

Deformations permutahedron to associahedron to cube Construction monotone path polytope tetrahedron Construction pivot polytope tetrahedron
Sequence of deformations (from a permutahedron to an associahedron, then to a cube) Construction of the monotone path polytope of the tetrahedron Construction of the max-slope pivot rule polytope of the tetrahedron

Images

Random polytopes

Projection sphere to plane Plot of beta-distribution
The projection of the uniform distribution on the sphere to the plane gives a β-distribution Plot of β-distribution for β = -0.5, β = 1, β = 10
epsilon-cap and epsilon-floating body Region outside epsilon-floating body (rotationaly symmetric distribution)
Construction of an ε-cap and of the ε-floating body Region outside the ε-floating body for a rotationaly symmetric distribution
Visible region from a point First order difference operator
Definition of the region visible from a point, outside the ε-floating body Computation of the first difference operator
Adjacency matrices of random edge polytopes for several probabilities
Adjacency matrices of random edge polytopes for several probabilities in the Erdos-Renyi model, n = 50

Monotone paths polytopes and pivot rule polytopes

Coherent monotone path Monotone path polytope as sum sections
Definition of the coherent monotone path associated to ω Construction of the monotone path polytope (of a tetrahedron) as a Minkowski sum of sections (of this tetrahedron)
Monotone path polytope via stereographic projection Monotone path polytope hypersimplex 4,2
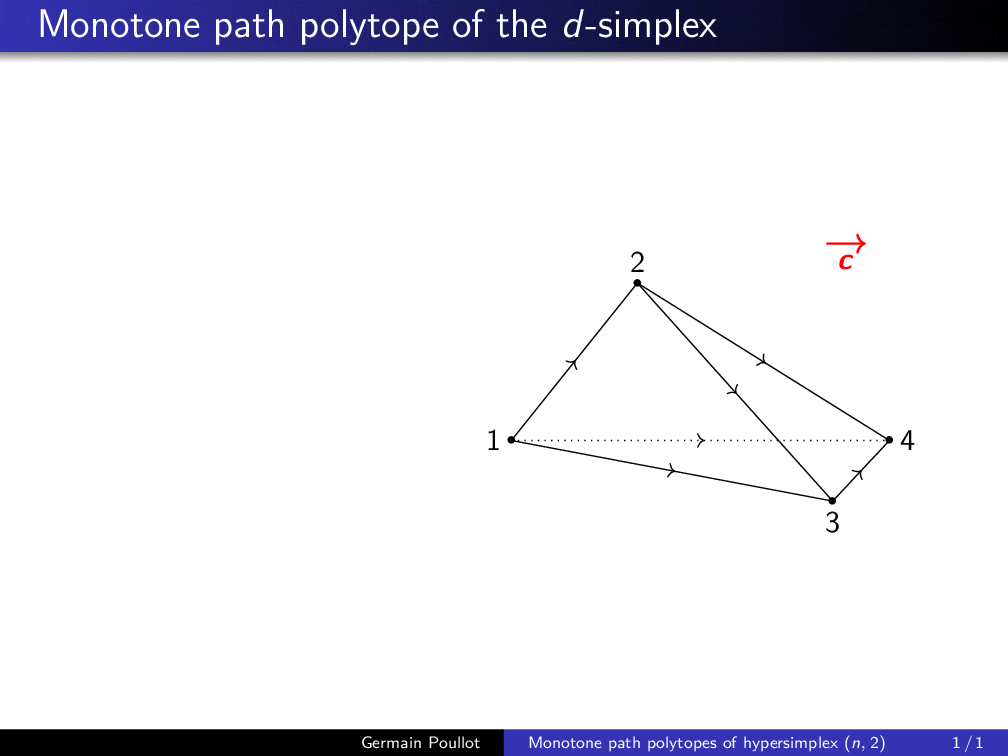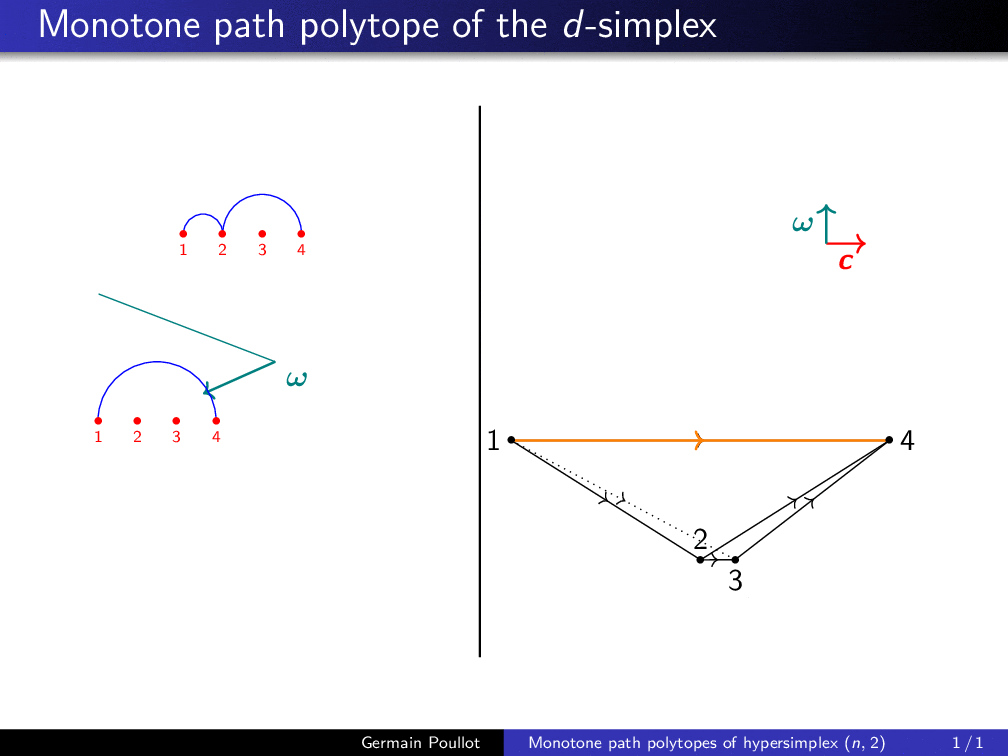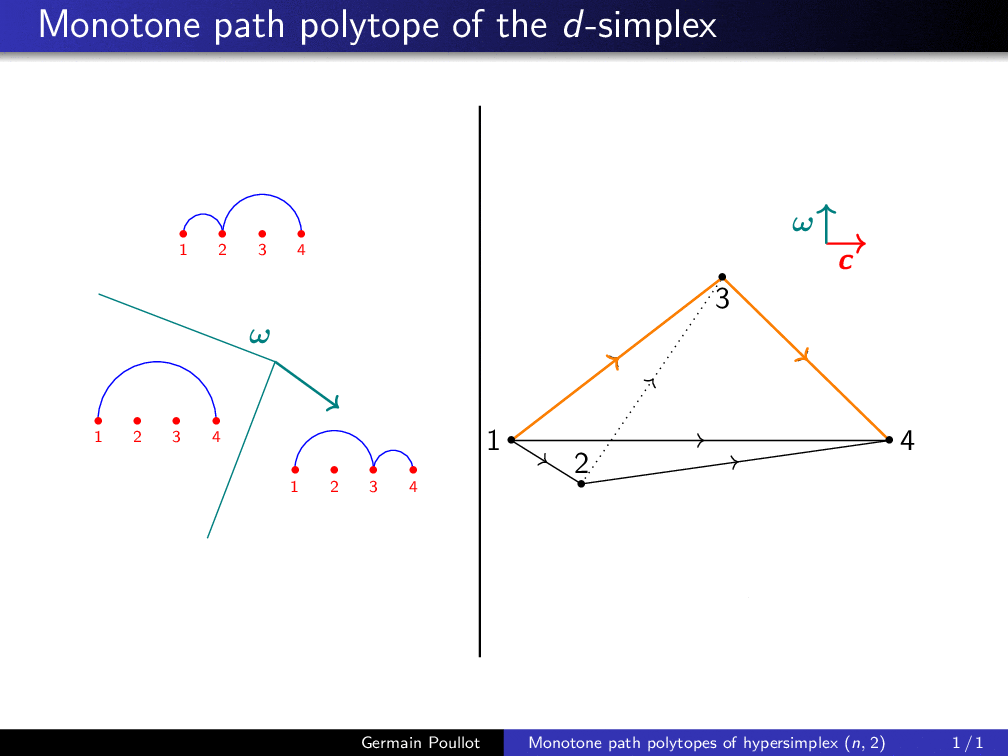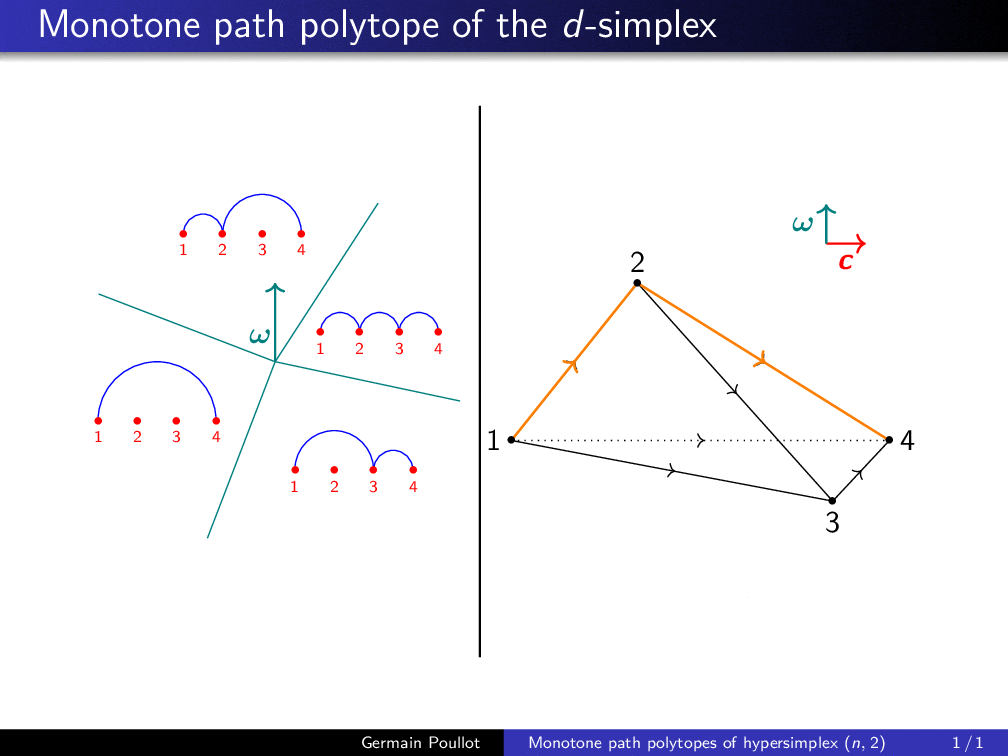
Construction of (the normal fan of) the monotone path polytope of a tetrahedron via the stereographic projection of the normal of of this tetrahedron Construction of the monotone path polytope of the hypersimplex Δ(4, 2), first combinatorially, then as the convex hull of points associated to all monotone paths (interior points correspond to non-coherent paths)
Monotone path polytope hypersimplex 5,2 Pivot polytope as sum sections
Monotone path polytope of the hypersimplex Δ(5, 2) (not actual geometry) Construction of the pivot rule polytope (of a tetrahedron) as a Minkowski sum of sections (of this tetrahedron)
Pivot polytope of cube Pivot polytope of tetrahedron
Pivot rule polytope of the standard 3-dimensional cube Pivot rule polytope of the standard 3-dimensional simplex

Special polytopes

Simplex of dimension 3 Pyramid over a square
Standard simplex of dimension 3 Pyramid over a square
Octahedron Strawberry
Octahedron Strawberry
Persimmon Cyclic polytope dimension 3
Persimmon Cyclic polytope of dimension 3 (its graph is not the complete graph)
Rhombor-dodecahedron Rhombo-hexagonal-dodechadron
Rhombo-dodecahedron: graphical zonotope of the 4-cycle Rhombo-hexagonal-dodecahedron: graphical zonotope of the 4-cycle with a chord
Associahedron (dimension 2) Graphical zonotope of the 4 cycle
The 2-dimensional associahedron, labeled by multiple combinatorial families Graphical zonotope of the 4 cycle
Lopsided cube Truncated lopsided cube
The lopsided cube of dimension 3 with its directed graph (its number of monotone paths per length is not unimodal) The truncated lopsided cube of dimension 3 (its number of monotone paths per length is not unimodal)
Simplcial polytope whose number of monotone paths per length is not unimodal
A simplcial polytope whose number of monotone paths per length is not unimodal
The first Sylvester simplices The 3D Sylvester simplices
The first Sylvester simplices constructed
as chimney polytopes and one-point extensions		 The layering of the 3D Sylvester simplices

Polytopes (general facts)

H- and V- polytopes Example bounded linear program
A (redundant) H-description and a (redundant) V-description of the same polytope Examples of (the bounded feasible domain of) a linear program
Wedge over a polytope
Wedge over a polytope in direction e_(n+1) - e_i

Submodular cone & Deformed permutahedra (a.k.a generalized permutahedra)

Permutahedra small dimensions Hexagon as a graphical zonotope
The first permutahedra, up to dimension 3 Hexagon: graphical zonotope of the 3-cycle
Braid and sylvester fans Construction of the GP-sum
The braid fan and the sylvester fan of dimension 2 The construction of the GP-sum
Submodular cone n = 3 Deformation cone rhombo-dodecahedron
The (intersection with an hyperplane of the) submodular cone for n = 3 (i.e. the deformation cone of the 3-dimensional permutahedron) The (intersection with an hyperplane of the) deformation cone of the rhombo-dodecahedron (i.e. of the graphical zonotope of the 4-cycle)
Submodular cone n = 3, as GP-sums Partition of the submodular cone n = 3 via generic GP-sums
The (intersection with an hyperplane of the) submodular cone for n = 3, as GP-sums Partition of the (intersection with an hyperplane of the) submodular cone for n = 3 via generic GP-sums
Part of the face lattice of the submodular cone n = 3 above the cube
Part of the face lattice of the submodular cone above the (deformation cone of the) cube

Minkowski sums and indecomposability

Minkowski decomposition of the regular hexagon Octahedron - proof of indecomposability
Regular written as Minkowski sums of indecomposable polytopes Proof of the indecomposability of an octahedron
Strawberry - proof of indecomposability Cuboctahedron - proof of indecomposability
Proof of the indecomposability of the Strawberry Proof of the indecomposability of the cuboctahedron
Persimmon - proof of indecomposability Kallay's example
Proof of the indecomposability of the Persimmon Kallay's example of combinatorially equivalent polytopes:
one decomposable, one indecomposable

Ehrhart theory, Triangulations

Chimney polytope One-point extension
Chimney polytope over a segment One-point extension over a triangle with one visible facet

Combinatorics

Bijection triangulations vs non-crossing arborescences Flippable quandrangles vs flippable triplets
Bijection between triangulations of a polygon and non-crossing arborescences Flips of quandrangles correspond to flip of arcs

Acyclic Orientations of Graphs

AO(tree) AO(G) for G with 4 edges
Graph of acyclic orientations of a tree with 4 edges Graph of acyclic orientations of a graph with 4 edges
AO(C_4) AO-fundamental involution
Graph of acyclic orientations of the 4-cycle Graph of acyclic orientations of a graph with 4 edges
adorned by the fundamental involution
Acyclic polynomials for K23 Replacing pattern
All possible acyclic polynomials for the complete bipartite graph K_{2, 3} Example of a replacing pattern (for the gluing of two paths of odd length)

Framing Lattices

Framing lattice of the weak order n = 4 Framing lattice of a planar framed digraph
Framing lattice of the weak order n = 4 Framing lattice of a planar framed digraph via linear extensions
Framing lattice of a non planar framed digraph Combinatorics of square intervals in framing lattices
Framing lattice of a non planar framed digraph (quotient of the weak order n = 4) Combinatorics of square intervals in framing lattices
Combinatorics of pentagonal intervals in framing lattices Combinatorics of hexagonal intervals in framing lattices
Combinatorics of pentagonal intervals in framing lattices Combinatorics of hexagonal intervals in framing lattices